Работа с градиентами.
Под градиентом в графике подразумевают плавный переход от одного цвета к другому, как правило, через промежуточные оттенки этих цветов. Например, градиентом можно считать цветовую гамму, которая начинается с красного цвета, далее следуют белее светлые оттенки красного пока всё это дело не перейдёт в белый цвет. Такой градиент называется переходом от красного до белого цвета. Например:

В данном случае, для наглядности использовано небольшое количество переходных цветов, но для красоты этого мало (хотя иногда бывает и необходимость и в таких грубых переходах). На самом деле подобный переход, только имеющий большее количество промежуточных оттенков, выглядит намного привлекательнее.

Обращаю ваше внимание на то, что практически любой, вернее сказать любой графический редактор, имеет инструментарий градиентов. Можно смело выделить общие принципы градиентов, а затем перейти к частностям и особенностям градиентов в Photoshop.
Для градиентов всегда общей чертой являлся тип градиента. В понятие «типа градиента», прежде всего, входят несколько основополагающих соглашений. В качестве первого соглашения принято выделять стартовые и конечные точки градиента. Под стартовой точной принято понимать цвет, с которого начинается переход, под конечной точкой – цвет к которому происходит переход. Кроме того, положение этих цветов на рисунке также играет немаловажную роль, но об этом позже.
Итак, первый тип градиента, который носит название линейный переход. Это классический случай, иллюстрацию которого можно наблюдать на рисунках выше. Смысл перехода заключается в том, что оттенки меняются вдоль прямой линии, проложенный от стартовой до конечной точки.

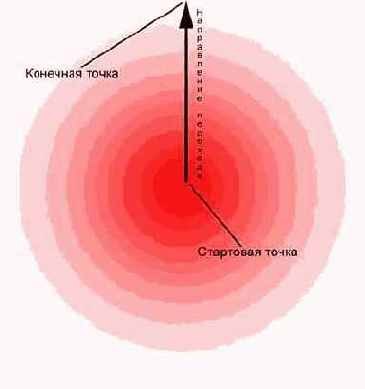
Далее следует следующий тип перехода – радиальный переход. В данном случае цвета меняются от стартовой точки до конечной, но по всем направлениям. Линия от стартовой до конечной точки является радиусом радиального перехода.
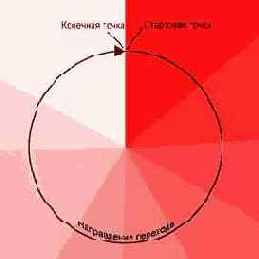
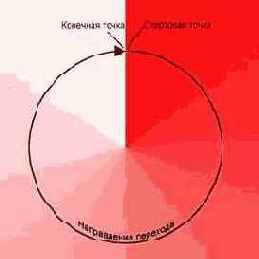
Потом переход, который носит название конического или углового. В данном случае направление перехода лежит на окружности, а стартовая точка по местоположению на изображении совпадает с конечной. Первая иллюстрация показывает принцип, а вторая реальность.
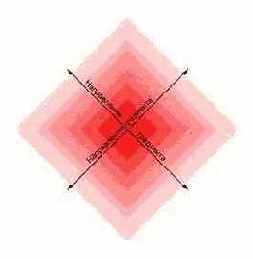
В качестве последнего распространённого типа градиента можно назвать ромбический (квадратный, square) или diamond (рука не поворачивается озвучить это по русски) переход. В данном случае трудно озвучить принцип на основании предыдущих определений. В этом случае мы имеем дело не со стартовой точкой, а с стартовой фигурой в виде прямоугольника. Преобразование цвета происходит от центра фигуры к краям. При небольшом количестве промежуточных цветов зрелище довольно жуткое, однако в полноценной палитре такой градиент приобретает интересный вид благодаря которому возникло название diamond (бриллиант).
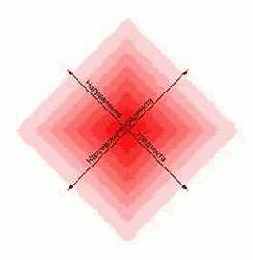
Градиенты могут состоять не только из двух основных цветов. В одном переходе может содержаться разумно большое количество ключевых промежуточных цветов. Применение в одном градиенте нескольких цветовых переходов позволяет создавать очень интересные эффекты.

Переход с несколькими ключевыми цветами бывает не только линейного типа. Такую возможность можно реализовать и во всех остальных перечисленных выше типах градиентов.
Градиенты в Photoshop
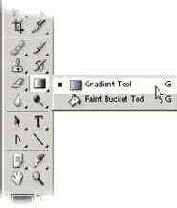
Photoshop предоставляет специальный инструмент для работы с градиентами. Он находится на панели инструментов в одной группе с инструментом Paint Bucket.Для того, что бы воспользоваться этим инструментом нужно совершить ряд действий.
1. Выбрать инструмент Gradient на панели инструментов.
2. Щёлкнуть мышкой на том месте изображения,где вы хотите поставить стартовую точку вашего градиента.
3. Не отпуская кнопку мыши, протяните направление градиента.
4. Там, где будет отпущена кнопка мыши вы установите конечную точку градиента.
Обязательно обратите внимание на следующую особенность градиента. Цветовой переход происходит от стартовой до конечной точки. Но на изображении может быть и область, которая находится до стартовой точки и после
конечной точки. В этом случае эффект будет несколько неожиданный. Та часть изображения которая находится до
стартовой точки окрасится в стартовый цвет градиента, а та часть изображения, которая идёт после конечной точки окрасится в конечный цвет градиента, соответствено между этими точками и будет находится сам градиент.
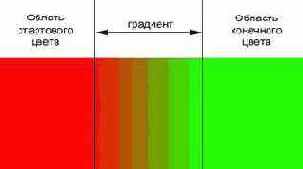
Данная особенность свойственна всем типам градиентов и варьируется в зависимости от типа градиента. В случае градиентов у которых переход цвета происходит от центра (радиальный и ромбический) весь рисунок, начиная от конечной точки будет заполнен конечным цветом градиента.
Управление градиентом, как и любым инструментом находится на палитре Options.
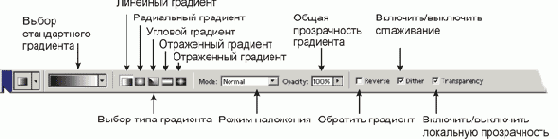
Photoshop имеет ряд заготовок градиентных переходов. Заготовка включает в себя понятие заранее созданного набора параметров для градиента, т.е. количества ключевых точек, цвета ключевых точек расстояние между ключевыми точками и многие другие, пока неизвестные нам параметры. Если щёлкнуть на треугольничке выпадающего меню заготовок, то можно узреть весь список заготовок, предоставленных нам создателями Photoshop. Этот список можно редактировать, удаляя и добавляя свои заготовки. Справа находится кнопочка [

1. Команда New Gradient вызывает окно редактирования параметров градиента
2. Команда Rename Gradient даёт новое название старым заготовкам градиентов.
3. Команда Delite Gradient удаляет заготовку.
4. Команда Text Only включяет режим палитры, при котором вместо иконок будут только подписи.
5. Команда Small Tambnails включяет режим палитры, при котором в палитре будет отображено содержимое в виде небольших по размеру иконок .
6. Команда Large Tambnails включяет режим палитры, при котором в палитре будет отображено содержимое в виде больших по размеру иконок .
7. Команда Small list включяет режим палитры, при котором в палитре будет отображено содержимое в виде небольших иконок и текстовой информации.
8. Команда Large listвключяет режим палитры, при котором в палитре будет отображено содержимое в виде больших иконок и текстовой информации.
9. Команда Preset Manager вызывает менеджер (интерфейс) позволяющий загрузить заготовки из файлов, сохранить в виде файлов, переименовать и удалить.
10. Команда Reset Gradients сбрасывает изменённые настройки заготовок до начальных значений параметров.
11. Команда Load Gradients загружает заготовки из файла. Полезно сохранять удачно получившиеся градиенты для дальнейшего использования.
12. Команда Save Gradients сохраняет настройки градиента в виде заготовки.
13. Команда Repalce Gradients змещает существующий градиент загружаемым.
14. Команда Color Harmonis 1 загружает набор градиентов, который создатели Photoshop считают гармоничным по цветовой гамме.
15. Команда Color Harmonis 2 загружает набор градиентов, который создатели Photoshop считают гармоничным по цветовой гамме. Серия №2.
16. Команда Metals загружает набор градиентов, иммитирующмх всевозможные металлические блески.
17. Команда Noise Samples загружает градиенты с некоторым цветовым "шумом".
18. Команда Pastels загружает градиенты пастельных тонов.
19. Команда Simple загружает совершенно простые градиенты.
20. Команда Special Effects загружает нечто визуально приятное.
21. Команда Spectrums загружает градиенты спектральных цветов.
Набор готовых градиентов это здорово, но порою нужно что-то особенное, своё. Для этого существует конструктор градиентов. Вызывается он просто - достаточно щёлкнуть по иконке заготовки на панели Options при выбранном инструменте Gradient. Вашему виду откроется следующее диалоговое окно.
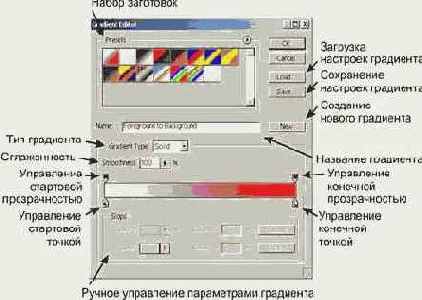
Настроить градиент можно на основании заготовок, для этого они и приведены, но это называется не настройка, а подстройка. Займёмся серьёзным делом. Для этого наберём какое-либо своё имя в поле имени и нажмём кнопку NEW. В результате этого действия возникнет новый градиент, являющийся полной копией старого, но имеющий своё название. Теперь поработаем над цветом. Для начала выделим статовый стопор (ползунок слева внизу), который отвечает за цвет стартовой точки. В нижней части окна станет активным маленькое окошко выбора цвета. У этого окошка есть меню, которое позволяет сделать следующее:
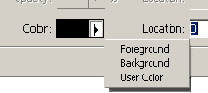
1. Foregraund Color - Установить в качестве стартового цвета основной цвет (выбирается на панели инструментов). Это означает, что стартовый цвет вашего градиента всегда будет такой же, как и выставленный вами основной цвет.
2. Background Color - Установить в качестве стартового цвета фоновый цвет (выбирается на панели инструментов). Это означает, что стартовый цвет вашего градиента всегда будет такой же, как и выставленный вами фоновый цвет.
3. User Color - Вы устанавливаете фиксированный стартовый цвет, который можно выбрать в открывшемся диалоговом окне если щёлкнуть по пиктограмме цвета.
Если вы устанавливаете в качестве стартового цвет Foreground или Background, то получаеете возможность в дальнейшем изменять цвета градиента не углубляясь в столь серьёзные настройки. Достаточно выбрать вашу заготовку в списке заготовок градиентов, затем установить основной или фоновый цвет (в зависимости от того, какие настойки вы задали в заготовке), и ваша заготовка возмёт цвета из палитры инструментов.
Точно таким же образом вы сможете установить цвет конечной точки градиента. Только вместо левого нижнего ползунка нужно выделить правый нижний.
Для добавления промежуточных ключевых цветов нужно просто щёлкнуть мышкой между ползунками стартового и конечного цвета. Затем выбираем цвет точно таким же образом как для стартовой и конечной точки.

Для промежуточных ключевых точек существует ещё несколько характеристик. Параметр Location (поле этого параметра расположено так же внизу диалогового окна) указывает на расстояние между этой точкой и стартовой точкой градиента. Это расстояние измеряется в процентах, а за 100% процентов принимается расстояние между стартовой и конечной точкой.
Вы наверное обратили внимание на появившиеся под образцом градиента маленькие ромбики. Эти ромбики показывают где находится середина перехода. Передвигая эти ромбики вы можете акцентировать переход на том или ином цвете. Добавлять ключевые точки можно в неограниченном количестве. Для того, что бы удалить промежуточный цвет нужно просто перетащить ползунок цвета за пределы окна.
Теперь настало время немного попрактиковаться. Попробуйте повторить созданные ниже рисунки.


После того, как это у вас получится, сохранение результат и предъявите преподавателю. Это часть вашего домашнего задания.
Есть ещё одно очень полезное свойство у градиента в Photoshop - это локальная, градиентная прозрачность. Название я выдумал жуткое, но на самом деле всё относительно просто. Для проведения эксперемента проведём следующие подготовительные действия. Откройте любой документ (рисунок). Далее создадим новую заготовку градиента, нажав кнопочку NEW в редакторе (конструкторе градиентов). У нас будет всего 2 ключевые точки - стартовая и конечная. Задайте обоим точкам одинаковый цвет, к примеру чёрный. Теперь обратите внимание на ползунки над образцом градиента. Это стартовая и конечная точка управления локальной прозрачностью или точнее говоря непрозрачностью. Щёлкните на левом верхнем ползунке (стартовая прозрачность градиента).
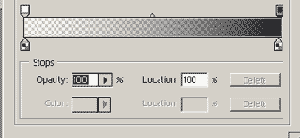
В нижней части окна станет доступным поле Opacity. По умолчанию этот параметр равен 100%, т.е. абсолютно непрозрачно. Установите значение opacity для стартовой точки равным 0. Теперь у вас появились шашечки, которые свидетельствуют о том, что прозрачность появилась. Если применить полученный градиент в "линейном типе" слева направо, то получится следующая картина:

Точно также как и в случае с ключевыми цветами, вы имеете возможность расставлять ключевые прозрачности в неограниченном количестве. Для этого достаточно просто щёлкнуть мышкой между стартовой и конечной прозрачностью, а затем задать необходимый вам параметр opacity для этой промежуточной ключевой точки. Основываясь на этом примере, прошу повторить следующие картинки:

Для получения резких границ можно использовать по две ключевые точки в одном месте (location). Ромбики между ползунками также помогут вам акцентировать прозрачность к началу градиента или к конечной точке. Орла вы сможете взять из папки sample находящейся в папке Adobe. Как только получится, сразу сохраняйте и приносите преподавателю на занятие. Это тоже домашнее задание.
Мы еще не разобрали выпадающее меню Gradient Type. Оно даёт вам возможность выбрать тип перехода. Всего два типа - solid и noise. Состоят в способе фофирования переходных цветов. В случае, если тип solid, то промежуточные пиксели (пиксели находящиеся между статовой точкой и конечной точкой) принимают значение промежуточных цветов (как вы помните пиксел имеет только одно значение - цвет). В случае если тип градиента noise то оттенок цвета получается при перемешивании пикселей начального и конечного цвета в разных пропорциях. Визуально это производит впечатление некоторого "шума".
Теперь, разобрав редактор градиентов вернёмся к палитре Options инструмента Gradient.

Теперь можно переключать тип градиента.
·

·

·

·

·

В Photoshop, кроме стандартных типов градиентов, присутствует ещё один тип - отражённый градиент. Он имитирует блеск на какой либо поверхности.
При нанесении градиента на изображение можно изменять прозрачность инструмента. Это то, что я назвал глобальной прозрачностью. действие такое же как и у прозрачности инструмента "Кисть". Опция REVERSE позволяет менять местами стартовую и конечную точку градиента. Опция Transparency включает или выключает прозрачность, настроенную в редакторе градиентов.