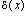Основы теории информации и передачи сигналов
       

Свойства обобщенных функций позволяют использовать


Приложение
Сведения из теории обобщенных функций
Свойства обобщенных функций позволяют использовать методы дифференциального и интегрального исчисления применительно к функциям, не обладающим свойством непрерывности.
К обобщенным функциям принято относить прежде всего дельта-функцию Дирака и ступенчатую функцию Хевисайда.
Дельта-функция
Определение:
Свойства обобщенных функций позволяют использовать
(1a)
Свойства обобщенных функций позволяют использовать
(1б)
Вариант определения дельта-функции с переменным параметром
Свойства обобщенных функций позволяют использовать
:
Свойства обобщенных функций позволяют использовать

где
Свойства обобщенных функций позволяют использовать
. (2)
Предел функции (2) при
Свойства обобщенных функций позволяют использовать
существует не при всех значениях х, однако всегда существует предел
Свойства обобщенных функций позволяют использовать
.
Любая операция над дельта-функцией подразумевает операцию над функцией вида
Свойства обобщенных функций позволяют использовать
с последующим нахождением предела при
Свойства обобщенных функций позволяют использовать
в конце вычислений.
Свойства дельта-функции
  1. “Селектирующее” свойство выражается в форме
    Свойства обобщенных функций позволяют использовать
    (3)

    2. где f(x) – любая непрерывная функция. Это легко доказать, приняв
    Свойства обобщенных функций позволяют использовать

    Подбором значения m в (2), можно уменьшить погрешность замены f(x) на f(a) до требуемого любого малого значения. Интегрирование достаточно выполнить лишь в окрестности точки a, поэтому символически записывают следующее соотношение:
    Свойства обобщенных функций позволяют использовать

    При
    Свойства обобщенных функций позволяют использовать
    последняя запись сводится к соотношению
    Свойства обобщенных функций позволяют использовать

  2. Свойство четности:

    3. Свойства обобщенных функций позволяют использовать
    (4)
  3. Изменение масштаба:

    4. Свойства обобщенных функций позволяют использовать
    (5)
  4. Свертка двух дельта-функций определяется как
    Свойства обобщенных функций позволяют использовать
    (6)
  5. Дифференцирование

Используем “аппроксимирующие” функции вида (2) и запишем
Свойства обобщенных функций позволяют использовать

Переход к пределу при
Свойства обобщенных функций позволяют использовать
приводит к соотношению
Свойства обобщенных функций позволяют использовать

В общем случае производной n-го порядка
Свойства обобщенных функций позволяют использовать
(7)
Свойства производных:
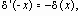
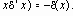
Свойства обобщенных функций позволяют использовать
(8)
Свойства обобщенных функций позволяют использовать
(9)
Определение дельта-функции через интеграл Фурье
Выразим значение функции f(x) в точке a в форме
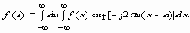
Свойства обобщенных функций позволяют использовать

Обозначив
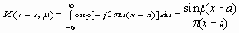
Свойства обобщенных функций позволяют использовать

и изменяя порядок интегрирования, с учетом четности дельта-функции получаем
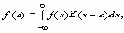
Свойства обобщенных функций позволяют использовать

где
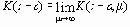
Свойства обобщенных функций позволяют использовать

Последний интеграл следует понимать в смысле
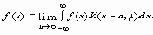
Свойства обобщенных функций позволяют использовать

При f(x)=1,
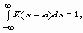
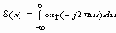
Свойства обобщенных функций позволяют использовать
поэтому дельта-функцию можно определить как
Свойства обобщенных функций позволяют использовать
(10)
т.е. как Фурье-образ от единицы.
Обратное соотношение выражается в виде
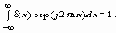
Свойства обобщенных функций позволяют использовать
(11)
Единичная ступенчатая функция
Определение ступенчатой функции имеет вид
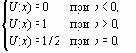
Свойства обобщенных функций позволяют использовать

Можно показать, что справедливо соотношение
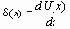
Свойства обобщенных функций позволяют использовать

Селектирующее свойство выражается в форме
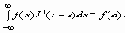
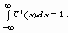
Свойства обобщенных функций позволяют использовать
(14)
Свойства обобщенных функций позволяют использовать

Примеры дифференцирования разрывных функций


  1. Пусть функция f(x) задана соотношением

    2. Свойства обобщенных функций позволяют использовать

    Тогда
    Свойства обобщенных функций позволяют использовать

  2. Знаковая функция sgn(x) по определению есть

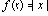
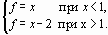
    3. Свойства обобщенных функций позволяют использовать

    или
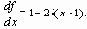
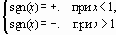
    Свойства обобщенных функций позволяют использовать

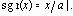
    Эту функцию можно выразить через обобщенные функции, а именно
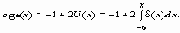
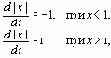
    Свойства обобщенных функций позволяют использовать

  3. Производные функции
    Свойства обобщенных функций позволяют использовать
можно выразить как
Свойства обобщенных функций позволяют использовать

или
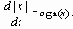
Свойства обобщенных функций позволяют использовать

При использовании дельта-функции можно записать
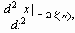
Свойства обобщенных функций позволяют использовать

т.е. излом графика дает вторую производную (кривизну) в виде функции
Свойства обобщенных функций позволяют использовать
.

Содержание раздела



Главная сайта