Основы теории информации и теории сигналов
1. Основы теории информации и теории сигналов
| 1.1. Основные понятия теории информации | |
| 1.2. Информационные характеристики источников дискретных сообщений | |
| 1.3. Принципы кодирования информации | |
| 1.4. Взаимосвязь теории информации, теории вероятностей и спектральной теории сигналов | |
| 1.5. Элементы спектральной теории сигналов | |
| 1.6. Принципы дискретизации непрерывных сигналов |
| Объекты информационной техники | |
| Виды сообщений в информационных системах | |
| Определение количества информации |
Информацию передают в виде сообщений. Сообщением называют информацию, выраженную в определенной форме и предназначенную для передачи от источника к адресату. Примерами сообщений служат тексты телеграмм, речь, музыка, телевизионное изображение, данные на выходе компьютера, команды в системе автоматического управления объектами и т.п.
Сообщения передают с помощью сигналов, которые являются носителями информации. Основным видом сигналов являются электрические сигналы. В последнее время всё большее распространение получают оптические сигналы, например, в волоконно-оптических линиях передачи информации.
В теории информации изучают свойства процессов, которые имеют место при передаче информации на расстояние при помощи сигналов. При этом важное значение имеют понятия качества и скорости передачи информации.
Качество передачи информации тем выше, чем меньше искажения информации на приёмной стороне. С увеличением скорости передачи информации требуется принимать специальные меры, препятствующие потерям информации и снижению качества передачи информации.
Объекты информационной техники
По функциональному назначению можно выделить основные классы объектов информационной техники:
- сети и системы связи и телекоммуникаций (телеграфные, телефонные, телевизионные, компьютерные и т.п.);
- информационно-измерительные системы (радионавигационные, радиолокационные, телеметрические и т.п.);
- системы преобразования информации (аналого-цифровые, цифро-аналоговые преобразователи, цифровые компьютеры и др.);
- информационно-поисковые системы и системы хранения информации на основе баз данных;
- системы экспериментального наблюдения и управления объектами.

Рис.
1.1.
Структурная схема системы передачи информации
Передатчик преобразует исходное сообщение A(x)
в сигнал


- выбор кратчайшего пути между источником и получателем сообщения;
- соблюдение системы приоритетов;
- накопление и хранение информации при отсутствии свободных каналов передачи;
- компьютерное управление всеми перечисленными функциями в автоматическом режиме.

ИС, ПС – источники и получатели сообщений,
К – кодеры, М – модуляторы, Дк – декодеры, Дм – демодуляторы. Вершины графа


- Анализ информационных характеристикисточников сообщений.
- Анализ и синтез сигналов и помех.
- Анализ и синтез помехоустойчивости методов передачи информации.
- Анализ и синтез корректирующих кодов (обнаружение и исправление ошибок).
- Анализ и синтез каналов передачи информации.

Пример графа информационной сети (пунктир – возможные линии связи, сплошные – примеры выбранных оптимальных линий связи) Виды сообщений в информационных системах Дискретное сообщение является конечной последовательностью отдельных символов. Для преобразования дискретного сообщения в сигнал необходимо выполнить операцию кодирования сообщения, при котором повышается скорость и помехоустойчивость передачи информации. Непрерывное сообщение определяется непрерывной функцией времени. Непрерывные сообщения можно передавать дискретными методами. Для этого непрерывный сигнал (сообщение) подвергаютдискретизации во времени и квантованию по уровню. На приёмной стороне выполняется восстановление непрерывной функции по дискретным отсчётам. При математическом описании сообщений формирование дискретных сообщений рассматривают как последовательный случайный выбор того или иного символа из алфавита источника сообщений, т.е. как формирование дискретной случайной последовательности. Формирование непрерывных сообщений представляет собой выбор реализаций (случайных функций) непрерывного случайного процесса. Основными информационными характеристиками являются количество информации в сообщениях, избыточность сообщений, энтропия, производительность источника сообщений, скорость передачи информации. Указанные характеристики рассмотрим для случая дискретных сообщений. Пусть объем алфавита A составляет m дискретных сообщений. Каждое сообщение включает n символов. В принятых обозначениях общее количество дискретных символов составляет
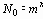
- сообщения большей протяжённости содержат, как правило, большее количество информации;
- если алфавит имеет больший объём, то каждое отдельное сообщение содержит больше информации;
- информация, полученная в нескольких сообщениях, должна удовлетворять условию аддитивности.
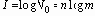
как мера количества информации. Формула Хартли не отражает случайного характера формирования сообщений. Чтобы устранить этот недостаток, необходимо связать количество информации в сообщениях с вероятностью появления символов. Эта задача была решена К. Шенноном в 1948 г. Следует упомянуть работы академика В. А. Котельникова о пропускной способности эфира и проволоки в электросвязи (1937 г.) и оптимальному приёму сигналов на фоне помех (1946 г.). Определение количества информации Пусть сообщение состоит из одного символа. Если вероятности появления всех символов одинаковы и равны P = 1/m, то количество информации, которое переносит символ, можно выразить как





- Энтропия источника дискретных сообщений есть величина вещественная, ограниченная и неотрицательная.
- Энтропия равна нулю, если с вероятностью единица выбирается один и тот же символ (неопределенность в поведении источника отсутствует).
- Энтропия максимальна, если все символы источника появляются независимо и с одинаковой вероятностью:





Эти потери информации характеризуются коэффициентом избыточности





| Свойства двоичных источников информации |

















Для источников с независимыми символами




















с неравновероятными символами Случай коррелированных равновероятных символов Пусть










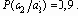
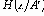
| Принципы обнаружения и исправления ошибок |
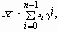
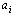
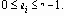
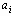
Число различных символов в коде называется основанием кода. Код с основанием 2 – бинарный, с другими основаниями – многопозиционный. Пример:

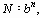
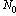
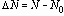
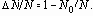
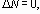
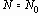

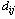
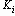
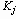
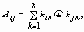
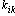
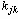
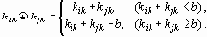
Например, если
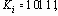
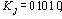
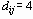
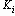
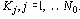
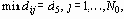
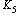
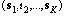


















случайного процесса


одно из m возможных значений. В теории стационарных случайных процессов одной из основополагающих является теорема Винера–Хинчина, устанавливающая взаимосвязькорреляционной функции R(c), где c – интервал, на котором вычисляется статистическая взаимосвязь значений сигнала, и спектральной плотности G(u) сигнала, зависящей от частоты u, в форме




-
В последней формуле подразумевается, что вся мощность сигнала сосредоточена на частотах (что характерно, например, для случайных сигналов в виде суммы периодических сигналов).

- Следует различать понятие спектра мощности и амплитудного спектра. Последнее понятие используется для анализа детерминированных сигналов в частотной области. Эти две величины, как будет показано далее, имеют разные физические размерности.
Таким образом показано, что энтропия источника сообщений, рассматриваемых как реализации гауссовского случайного процесса, определяется спектральной плотностью процесса. Для гауссовского процесса энтропия вычисляется по формуле (12). Следовательно, информационные характеристики передаваемых сообщений определяются спектральными характеристиками сигналов. 1.5. Элементы спектральной теории сигналов
Спектральное представление позволяет перейти от описания сигналов в области независимой переменной (времени) к частотной области.Ряды Фурье Преобразование Фурье Дискретное преобразование Фурье Финитное преобразование Фурье Математическое описание систем передачи и обработки сигналов Детерминированные и стохастические сигналы сигналов
Теорема о производной. Еслито (27) 5. Свойство четности и нечетности. Если
(27) 5. Свойство четности и нечетности. Если то в случае, когда s(x) четная функция, имеем
то в случае, когда s(x) четная функция, имеем – четная функция; при s(x) нечетной
– четная функция; при s(x) нечетной – нечетная функция. 6. Свойство подобия.
– нечетная функция. 6. Свойство подобия. (28) где a – постоянная. 7. Сохранение энергии.
(28) где a – постоянная. 7. Сохранение энергии. (29) Из этого соотношения следует, что
(29) Из этого соотношения следует, что для любых сигналов
для любых сигналов и
и , имеющих спектры
, имеющих спектры и
и . 8. Спектр свертки:
. 8. Спектр свертки: (30) Таким образом, преобразование Фурье, примененное к свертке двух сигналов, равно произведению спектров этих сигналов. Дискретное преобразование Фурье При обработке последовательности отсчётов сигнала интегральные соотношения следует заменить соответствующими операциями дискретного суммирования. Алгоритмы преобразования Фурье дискретной последовательности отсчётов s(p), имеющей конечную длину,
(30) Таким образом, преобразование Фурье, примененное к свертке двух сигналов, равно произведению спектров этих сигналов. Дискретное преобразование Фурье При обработке последовательности отсчётов сигнала интегральные соотношения следует заменить соответствующими операциями дискретного суммирования. Алгоритмы преобразования Фурье дискретной последовательности отсчётов s(p), имеющей конечную длину, сводятся к вычислению конечного числа коэффициентов S(q),
сводятся к вычислению конечного числа коэффициентов S(q), согласно соотношению
согласно соотношению (31) Обратимся к выражению (21) и сравним его с (31). Формула (31) представляет собой дискретную аппроксимацию преобразования (21), при которой функция s(x) заменяется ступенчатой функцией
(31) Обратимся к выражению (21) и сравним его с (31). Формула (31) представляет собой дискретную аппроксимацию преобразования (21), при которой функция s(x) заменяется ступенчатой функцией в пределах протяженности элемента дискретизации. Таким образом, следует помнить, что выражение (31) есть приближение, качество которого должно улучшаться при увеличении N и соответствующем уменьшении шага дискретизации Dx. Дискретное преобразование Фурье (ДПФ) обычно вычисляют при условии
в пределах протяженности элемента дискретизации. Таким образом, следует помнить, что выражение (31) есть приближение, качество которого должно улучшаться при увеличении N и соответствующем уменьшении шага дискретизации Dx. Дискретное преобразование Фурье (ДПФ) обычно вычисляют при условии , т.е.
, т.е. (32) где
(32) где Можно доказать, что для ядра преобразования (32) выполняется следующее тождество:
Можно доказать, что для ядра преобразования (32) выполняется следующее тождество: При этом обратное ДПФ (ОДПФ) определяется в форме
При этом обратное ДПФ (ОДПФ) определяется в форме (33) Свойства ДПФ можно получить из формул (24) – (30), имея в виду дискретный характер последовательности отсчётов сигнала. Финитное преобразование Фурье Всякий реальный сигнал имеет ограниченную протяженность. При этом вместо обычного преобразования Фурье
(33) Свойства ДПФ можно получить из формул (24) – (30), имея в виду дискретный характер последовательности отсчётов сигнала. Финитное преобразование Фурье Всякий реальный сигнал имеет ограниченную протяженность. При этом вместо обычного преобразования Фурье (34) имеем финитное преобразование в конечных пределах
(34) имеем финитное преобразование в конечных пределах где 2X – интервал регистрации сигнала. Для случая непрерывного изменения независимой переменной x с учётом (30) можно записать:
где 2X – интервал регистрации сигнала. Для случая непрерывного изменения независимой переменной x с учётом (30) можно записать: , (35) где
, (35) где – прямоугольная функция протяженностью 2X. Отличие (35) от идеального преобразования Фурье (21) иллюстрируется на рис. 1.6 для отрезка сигнала протяженности L=2X. Заметим, что середина отрезка L при этом смещена по горизонтальной оси на интервал X.
– прямоугольная функция протяженностью 2X. Отличие (35) от идеального преобразования Фурье (21) иллюстрируется на рис. 1.6 для отрезка сигнала протяженности L=2X. Заметим, что середина отрезка L при этом смещена по горизонтальной оси на интервал X.
Согласно свойству преобразования Фурье (25), это вызывает фазовый сдвиг 2p uX, пропорциональный значениям частоты u, но не изменяет модуль спектра.Рис. 1.6. Изменения спектра при ограниченной протяженности сигнала Для случая дискретных отсчётов, взятых в точках
 получим спектральные линии на дискретных частотах
получим спектральные линии на дискретных частотах Частота
Частота называется фундаментальной частотой финитного преобразования Фурье. При этом
называется фундаментальной частотой финитного преобразования Фурье. При этом (36) т.е. финитное преобразование Фурье связано с коэффициентами
(36) т.е. финитное преобразование Фурье связано с коэффициентами ряда Фурье, а именно:
ряда Фурье, а именно: Иначе говоря, финитное преобразование Фурье сводится к нахождению коэффициентов ряда Фурье для функции s(x), периодически продолженной с периодом
Иначе говоря, финитное преобразование Фурье сводится к нахождению коэффициентов ряда Фурье для функции s(x), периодически продолженной с периодом (рис. 1.7). При нецелом числе периодов, укладывающихся на отрезке L, происходит искажение спектра.
(рис. 1.7). При нецелом числе периодов, укладывающихся на отрезке L, происходит искажение спектра. Рис. 1.7. Трансляция отрезков сигнала ограниченной протяженности Математическое описание систем передачи и обработки
Рис. 1.7. Трансляция отрезков сигнала ограниченной протяженности Математическое описание систем передачи и обработки
сигналов В системах передачи и обработки сигналов осуществляется преобразование входных сигналовв выходные . Характеристики преобразования могут быть заданными (например, при фильтрации сигналов) или должны быть исследованы (например, при анализе характеристик линий передачи информации). Во всех случаях используются основные положения теории систем. Наиболее важными являются линейные системы, подчиняющиеся принципу суперпозиции:
. Характеристики преобразования могут быть заданными (например, при фильтрации сигналов) или должны быть исследованы (например, при анализе характеристик линий передачи информации). Во всех случаях используются основные положения теории систем. Наиболее важными являются линейные системы, подчиняющиеся принципу суперпозиции: , (37) где a и b – постоянные, T – оператор системы. Импульсной характеристикой (реакцией) системы, по определению, называется функция
, (37) где a и b – постоянные, T – оператор системы. Импульсной характеристикой (реакцией) системы, по определению, называется функция , (38) где
, (38) где – дельта-функция. Обычно независимой переменной x является время. Систему называют стационарной или инвариантной во времени, если при выполнении условия
– дельта-функция. Обычно независимой переменной x является время. Систему называют стационарной или инвариантной во времени, если при выполнении условия (39) следует, что
(39) следует, что , где c - произвольный сдвиг. Импульсная характеристика инвариантной во времени системы с учетом (38), очевидно, подчиняется соотношению
, где c - произвольный сдвиг. Импульсная характеристика инвариантной во времени системы с учетом (38), очевидно, подчиняется соотношению . Входной сигнал можно представить последовательностью дельта-функций:
. Входной сигнал можно представить последовательностью дельта-функций: , (40) где
, (40) где . Сигнал на выходе системы из (38) – (40) определяется выражением
. Сигнал на выходе системы из (38) – (40) определяется выражением . В результате выходной сигнал определяется интегралом свёртки
. В результате выходной сигнал определяется интегралом свёртки . (41) Пусть существует преобразование Фурье сигнала
. (41) Пусть существует преобразование Фурье сигнала и импульсной характеристики системы
и импульсной характеристики системы .
.
Используя свойства преобразования Фурье, можно доказать теорему о свёртке (30):. Поскольку , то в спектральной области
, то в спектральной области . (42) Функция
. (42) Функция (43) называется частотной характеристикой системы. Детерминированные и стохастические сигналы Преобразование Фурье (21) содержит полную информацию о сигнале s(x) в частотном представлении. Если сигнал s(x) является реализацией случайного процесса {s(x)}, то результат преобразования (21) будет изменяться от сигнала к сигналу (“от опыта к опыту”). Неизменной характеристикой ансамбля реализаций {s(x)} стационарного эргодического случайного процесса является спектральная плотность
(43) называется частотной характеристикой системы. Детерминированные и стохастические сигналы Преобразование Фурье (21) содержит полную информацию о сигнале s(x) в частотном представлении. Если сигнал s(x) является реализацией случайного процесса {s(x)}, то результат преобразования (21) будет изменяться от сигнала к сигналу (“от опыта к опыту”). Неизменной характеристикой ансамбля реализаций {s(x)} стационарного эргодического случайного процесса является спектральная плотность (44) где угловые скобки обозначают усреднение по ансамблю реализаций (индексу k). Спектральная плотность характеризует значение среднего квадрата процесса: площадь под графиком спектральной плотности на произвольном частотном интервале
(44) где угловые скобки обозначают усреднение по ансамблю реализаций (индексу k). Спектральная плотность характеризует значение среднего квадрата процесса: площадь под графиком спектральной плотности на произвольном частотном интервале равна среднему квадрату процесса в этой полосе частот. Наряду с понятием спектральной плотности часто используют соответствующее понятие энергетического спектра. Спектральная плотность стационарного эргодического случайного процесса связана с корреляционной функцией
равна среднему квадрату процесса в этой полосе частот. Наряду с понятием спектральной плотности часто используют соответствующее понятие энергетического спектра. Спектральная плотность стационарного эргодического случайного процесса связана с корреляционной функцией этого процесса преобразованием Фурье:
этого процесса преобразованием Фурье: (45) где
(45) где (46) Соотношение (45) носит название теоремы Винера-Хинчина. Поскольку автокорреляционная функция (46) является чётной функцией, спектральная плотность (45) является действительной чётной функцией. Таблица 1. Основные величины и типичные единицы их измерения
(46) Соотношение (45) носит название теоремы Винера-Хинчина. Поскольку автокорреляционная функция (46) является чётной функцией, спектральная плотность (45) является действительной чётной функцией. Таблица 1. Основные величины и типичные единицы их измерения
1.6. Принципы дискретизации непрерывных сигналовВеличина Обозначение Единица измерения 1. Сигнал s(x) В (Вольт) 2. Амплитудный спектр (АС) 

3. Квадрат модуля АС 

4. Спектральная плотность 

5. Корреляционная функция 

Пусть функция s(x) определяет исходный непрерывный сигнал. Операция дискретизации заключается в выполнении преобразования видаДискретизация узкополосных сигналов Влияние формы элемента дискретизации где в простейшем случае апертурная функция элемента дискретизацииh(x) имеет вид (47) 2b – ширина элемента дискретизации,
(47) 2b – ширина элемента дискретизации, –функция дискретизации, D x – шаг дискретизации,
–функция дискретизации, D x – шаг дискретизации, – нормирующий множитель, такой, что площадь под графиком d(x) равна единице. Вид функций h(x) и d(x) иллюстрируются на рис. 1.8.
– нормирующий множитель, такой, что площадь под графиком d(x) равна единице. Вид функций h(x) и d(x) иллюстрируются на рис. 1.8. Рис. 1.8.
Рис. 1.8.
Прямоугольная функция элемента дискретизации (а)
и функция дискретизации (б) Сигнал s(x) можно представить последовательностью импульсов протяженностьюимеющих амплитуды, равные значениям сигнала в точках . Тогда получим ступенчатую функцию, показанную на рис. 1.9, а именно
. Тогда получим ступенчатую функцию, показанную на рис. 1.9, а именно (48)
(48) Рис. 1.9. Ступенчатая аппроксимация непрерывного сигнала После перехода к пределу при
Рис. 1.9. Ступенчатая аппроксимация непрерывного сигнала После перехода к пределу при получим
получим (49) Такое преобразование является операцией свертки, которая имеет следующие важные свойства:
(49) Такое преобразование является операцией свертки, которая имеет следующие важные свойства:
- дистрибутивность

- коммутативность

- ассоциативность
Подчеркнем, что при условии существования интеграла (49) операция свертки не вносит ограничений на вид апертурной функции элемента дискретизации h(x). Процесс дискретизации удобно рассматривать в частотном представлении, получаемом в результате преобразования Фурье исходного сигнала. Функция дискретизации определяется в частотной области следующим выражением: (50) где
(50) где обозначает операцию преобразования Фурье,
обозначает операцию преобразования Фурье, . Вид функции D(u) показан на рис. 1.10. Таким образом, процесс выборки дискретных значений сигнала вызывает появление спектральных порядков
. Вид функции D(u) показан на рис. 1.10. Таким образом, процесс выборки дискретных значений сигнала вызывает появление спектральных порядков
 Рис. 1.10. Функция дискретизации и её частотное представление Дискретизованный сигнал имеет вид произведения двух функций, поэтому, согласно теореме о свертке, его спектр равен свертке спектров:
Рис. 1.10. Функция дискретизации и её частотное представление Дискретизованный сигнал имеет вид произведения двух функций, поэтому, согласно теореме о свертке, его спектр равен свертке спектров: . Поскольку с учетом (50) и свойств частотной симметрии преобразования Фурье (см. разд 1.5) можно записать, что
. Поскольку с учетом (50) и свойств частотной симметрии преобразования Фурье (см. разд 1.5) можно записать, что , спектр дискретизованного сигнала представляет собой спектр исходного сигнала, периодически повторенного (перенесенного) по частотной оси с шагом
, спектр дискретизованного сигнала представляет собой спектр исходного сигнала, периодически повторенного (перенесенного) по частотной оси с шагом , как это иллюстрируется на рис. 1.11, включая диапазон отрицательных частот. Теорема дискретизации формулируется следующим образом: Для того, чтобы спектр исходного сигнала в области частот
, как это иллюстрируется на рис. 1.11, включая диапазон отрицательных частот. Теорема дискретизации формулируется следующим образом: Для того, чтобы спектр исходного сигнала в области частот не искажался в процессе дискретизации, необходимо и достаточно выполнение неравенства
не искажался в процессе дискретизации, необходимо и достаточно выполнение неравенства , где
, где – наибольшая частота в спектре синала. Спектр сигнала, очевидно, можно выразить в форме
– наибольшая частота в спектре синала. Спектр сигнала, очевидно, можно выразить в форме (51) Выделим из этого спектра частотный интервал
(51) Выделим из этого спектра частотный интервал и выполним обратное преобразование Фурье.
и выполним обратное преобразование Фурье.
В результате получим(52) Отсюда следует теорема Шеннона: если для частоты дискретизации справедливо неравенство
справедливо неравенство то сигнал s(x) восстанавливается однозначно по его дискретным значениям
то сигнал s(x) восстанавливается однозначно по его дискретным значениям
 Рис. 1.11. Формирование спектра при дискретизации сигнала Функция
Рис. 1.11. Формирование спектра при дискретизации сигнала Функция называется интерполяционной функцией Шеннона. Дискретизация узкополосных сигналов Модель типичного узкополосного сигнала имеет вид
называется интерполяционной функцией Шеннона. Дискретизация узкополосных сигналов Модель типичного узкополосного сигнала имеет вид (53) где
(53) где – фоновая составляющая,
– фоновая составляющая, – огибающая, изменяющиеся медленно по сравнению с периодом
– огибающая, изменяющиеся медленно по сравнению с периодом e – начальная фаза в точке x = 0,
e – начальная фаза в точке x = 0, – частота, n(x) – аддитивный шум. В результате дискретизации получаем сигнал
– частота, n(x) – аддитивный шум. В результате дискретизации получаем сигнал при этом спектр сигнала определяется выражением
при этом спектр сигнала определяется выражением (54) Здесь N(u) обозначает амплитудный спектр аддитивного шума, H(u) – преобразование Фурье апертурной функции элемента дискретизации. Для функции вида (47) прямоугольной формы и
(54) Здесь N(u) обозначает амплитудный спектр аддитивного шума, H(u) – преобразование Фурье апертурной функции элемента дискретизации. Для функции вида (47) прямоугольной формы и нулевые значения H(u) имеют место на частотах
нулевые значения H(u) имеют место на частотах . Спектр дискретизованного сигнала имеет вид, показанный на рис. 1.12. При обработке спектра обычно выделяют составляющую
. Спектр дискретизованного сигнала имеет вид, показанный на рис. 1.12. При обработке спектра обычно выделяют составляющую
 Рис. 1.12. Формирование спектра при дискретизации узкополосного сигнала Рассмотрим методику выбора шага дискретизации узкополосного сигнала. Если частота
Рис. 1.12. Формирование спектра при дискретизации узкополосного сигнала Рассмотрим методику выбора шага дискретизации узкополосного сигнала. Если частота гармонической составляющей априорно известна, то шаг дискретизации Dx определяется согласно теореме дискретизации, а именно, нужно выполнить условие
гармонической составляющей априорно известна, то шаг дискретизации Dx определяется согласно теореме дискретизации, а именно, нужно выполнить условие , т.е.
, т.е. . Таким образом, шаг дискретизации должен быть меньше половины периода гармонического сигнала. Если сигнал s(x) не является строго гармоническим и имеет протяженный спектр с граничной частотой
. Таким образом, шаг дискретизации должен быть меньше половины периода гармонического сигнала. Если сигнал s(x) не является строго гармоническим и имеет протяженный спектр с граничной частотой , то выбор шага дискретизации определяется по теореме дискретизации:
, то выбор шага дискретизации определяется по теореме дискретизации: . Для уменьшения влияния спектра шума, попадающего из соседних спектральных порядков (рис. 1.12), нужно настолько уменьшить шаг дискретизации, чтобы он не превышал значения
. Для уменьшения влияния спектра шума, попадающего из соседних спектральных порядков (рис. 1.12), нужно настолько уменьшить шаг дискретизации, чтобы он не превышал значения , где
, где – составляющая шума с наибольшей частотой. Следует иметь в виду, что вследствие стохастического характера шума можно строго определить его спектр мощности, но не амплитудный спектр.
– составляющая шума с наибольшей частотой. Следует иметь в виду, что вследствие стохастического характера шума можно строго определить его спектр мощности, но не амплитудный спектр.
Поэтому результат преобразования Фурье шума может существенно изменяться от реализации к реализации. Некоррелированный шум имеет спектр бесконечной протяженности. Поэтому перед дискретизацией сигнала необходимо выполнить низкочастотную фильтрацию для получения “окрашенного” шума с граничной частотой. Влияние формы элемента дискретизации Операция дискретизации определяется формулой Выше был рассмотрен случай ступенчатой аппроксимации нулевого порядка, как это показано на рис. 1.9. Функция h(x), вообще говоря, может иметь произвольную форму. Однако в любом случае нужно иметь в виду, что форма и протяженность функции h(x) влияют на спектр сигнала за счет умножения спектра этого сигнала на функцию
Выше был рассмотрен случай ступенчатой аппроксимации нулевого порядка, как это показано на рис. 1.9. Функция h(x), вообще говоря, может иметь произвольную форму. Однако в любом случае нужно иметь в виду, что форма и протяженность функции h(x) влияют на спектр сигнала за счет умножения спектра этого сигнала на функцию (рис. 1.12). Приведем простой пример. Пусть
(рис. 1.12). Приведем простой пример. Пусть Соответствующая функция в спектральной области будет равна
Соответствующая функция в спектральной области будет равна В этом несложно убедиться непосредственным интегрированием функции косинуса:
В этом несложно убедиться непосредственным интегрированием функции косинуса: Поэтому составляющие спектра сигнала при u > 0 будут ослаблены вплоть до полного подавления на частоте
Поэтому составляющие спектра сигнала при u > 0 будут ослаблены вплоть до полного подавления на частоте (рис. 1.12). Таким образом, можно сделать следующие выводы. Влияние размера элемента дискретизации на спектральную составляющую с частотой u тем меньше, чем меньше отношение
(рис. 1.12). Таким образом, можно сделать следующие выводы. Влияние размера элемента дискретизации на спектральную составляющую с частотой u тем меньше, чем меньше отношение , где
, где