"Пример моделирования 2Е. Задача об управлении производством"
Постановка задачи. На трикотажной фабрике 50 швейных машин работают по 8 ч в день и по 5 дней в неделю. Любая из этих машин может в любой момент времени выйти из строя. В этом случае ее заменяют резервной машиной, причем либо сразу, либо по мере ее появления. Тем временем сломанную машину отправляют в ремонтную мастерскую, где ее чинят и возвращают в цех, но уже в качестве резервной.
В существующем замкнутом цикле движения машин легко выделить четыре фазы (рис.2Е.1).
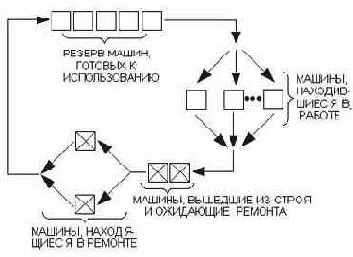
Рис.2Е.1
На рисунке квадраты представляют машины, находящиеся в работе или в резерве. Перечеркнутые квадраты представляют собой машины либо ремонтируемые, либо ожидающие ремонта. Показаны две машины в ремонте; предполагается, что два человека могут параллельно чинить машины. Всего в системе находятся 59 машин (две в ремонте, две ждут ремонта, 50 в работе и пять готовы к использованию).
Управляющий хочет знать, сколько рабочих следует нанять для работы в мастерской, сколько машин следует иметь в резерве, какую платить за это арендную плату, чтобы резервными машинами можно было подменить 50 собственных. Цель - минимизация стоимости производства.Оплата рабочих в мастерской 3,75 доллара в час. За машины, находящиеся в резерве, надо платить по 30 долларов в день. Почасовой убыток при использовании менее 50 машин в производстве оценивается примерно в 20 долларов на машину. Этот убыток возникает из-за снижения производства.
Опыт эксплуатации подсказывает, что на ремонт сломанной машины уходит примерно 7 ± 3 ч, распределение равномерное. Когда машину используют в производстве, время наработки до отказа распределено равномерно и составляет 157 ± 25 ч. Время, необходимое для перевозки машины из цеха в мастерскую и обратно, мало, и его не учитывают.
Между рабочими в мастерской не делают никаких различий. Не делают различий также и между машинами. Иными словами, распределение времени ремонта не зависит от того, кто какую машину ремонтирует. Распределение времени наработки до отказа одинаково как для собственных, так и для арендуемых машин.
Плата за арендуемые машины не зависит от того, используют их или они простаивают. По этой причине не делают попыток увеличить число собственных машин в работе в любой период времени. Предполагаем, что машину снимают с работы только в том случае, если она ломается. Необходимо построить на GPSS модель такой системы и исследовать на ней расходы при различном числе арендуемых машин, доступных управляющему. Найдите такую величину, которая минимизирует стоимость эксплуатации системы. Метод построение модели. Как и в случае 2D, предполагается, что в первую очередь следует разобраться в том, какие ограничения существуют в системе, а затем определить, какие элементы GPSS следует использовать для удовлетворения этих ограничений. В нашей системе (см. рис. 2Е.1) существуют три ограничения:
- Число рабочих в мастерской.
- Максимальное число швейных машин, одновременно находящихся в производстве.
- Общее число машин, циркулирующих в системе.
Теперь транзакт ожидает (если в этом есть необходимость) входа в многоканальное устройство MEN (рабочие мастерской). Войдя в это многоканальное устройство, транзакт играет роль ремонтируемой машины. Когда он уходит из этого многоканального устройства,тем самым освобождая рабочего, последний может приняться за ремонт следующей машины. Тем временем транзакт вновь возвращается в ту точку модели, в которой он снова начинает делать попытки войти в многоканальное устройство NOWON. Общее число машин, циркулирующих в системе, равно 50 собственным машинам плюс некоторое число арендуемых для резерва. Это число следует задавать до начала прогона модели с использованием ограничителя блока GENERATE. Единственным недостающим элементом модели теперь является таймер. Обратите внимание на то, что многоканальное устройство NOWON можно рассматривать как 50 операторов швейных машин. Эта точка зрения отвечает тому ограничению, что одновременно не могут работать более 50 швейных машин. Эта довольно сложная задача на GPSS может быть промоделирована очень просто. Модель этой же системы на языке FORTRAN значительно сложнее. Таблица определений. Единица времени: 1 ч.
Таблица 24.1. Таблица определений примера моделирования 2Е.
| Элементы GPSS | Интерпретация | ||||||
Транзакты:
|
 
|
||||||
Многоканальные устройства:
|
 
|
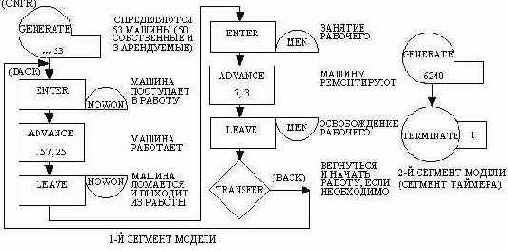
| BLOCK NUMBER *LOC OPERATION A,B,C,D,E,F,G COMMENTS SIMULATE * * STORAGE CAPACITY DEFINITION(S) * STORAGE S$MEN,3/S$NOWON,50 3 MEN; MAX OF 50 MATCH`S RUNNING * * MODEL SEGMENT 1 * 1 CNTRL GENERATE ,,,53 PROVIDE 53 MACHINES (50 OWNED; 3 RENTED) 2 BACK ENTER NOWON MACHINE GOES INTO PRODUCTION 3 ADVANCE 157,25 MACHINE IS RUNNING 4 LEAVE NOWON MACHNE FAULTS; COMES OUT OF PRODUCTION 5 ENTER MEN CAPTURE A REPAIR MAN 6 ADVANCE 7,3 MACHINE IS BEING REPAIRED 7 LEAVE MEN FREE THE REPAIRMAN 8 TRANSFER ,BACK * * MODEL SEGMENT 2 * 9 GENERATE 6240 TIMER COMES AFTER 3 YEARS (40-HOUR WEEKS) 10 TERMINATE 1 SHUT OFF THE RUN * * CONTROL CARDS, BLOCK OPERAND RE-DEFS, AND STG CAPACITY RE-DEFS * START 1 START THE 1ST RUN 1 CNTRL GENERATE ,,,54 SET RENTED MACHINES = 4 FOR 2ND RUN MULTIPLE DEFINITION OF SYMBOL IN ABOVE CARD CLEAR CLEAR FOR 2ND RUN START 1 START THE 2ND RUN 1 CNTRL GENERATE ,,,55 SET RENTED MACHINES = 5 FOR 3RD RUN MULTIPLE DEFINITION OF SYMBOL IN ABOVE CARD CLEAR CLEAR FOR 3RD RUN START 1 START THE 3RD RUN STORAGE S$MEN,4 SET REPAIRMEN HIRED = 4 FOR 4TH RUN 1 CNTRL GENERATE ,,,53 SET RENTED MACHINES = 3 FOR 4TH RUN MULTIPLE DEFINITION OF SYMBOL IN ABOVE CARD CLEAR CLEAR FOR 4TH RUN START 1 START THE 4TH RUN 1 CNTRL GENERATE ,,,54 SET RENTED MACHINES = 4 FOR 4TH RUN MULTIPLE DEFINITION OF SYMBOL IN ABOVE CARD CLEAR CLEAR FOR 5TH RUN START 1 START THE 5TH RUN 1 CNTRL GENERATE ,,,55 SET RENTED MACHINES = 5 FOR 6TH RUN MULTIPLE DEFINITION OF SYMBOL IN ABOVE CARD CLEAR CLEAR FOR 6TH RUN START 1 START THE 6TH RUN STORAGE S$MEN,5 SET REPAIRMEN HIRED = 5 FOR 4TH RUN 1 CNTRL GENERATE ,,,53 SET RENTED MACHINES = 3 FOR 7TH RUN MULTIPLE DEFINITION OF SYMBOL IN ABOVE CARD CLEAR CLEAR FOR 7TH RUN START 1 START THE 7TH RUN 1 CNTRL GENERATE ,,,54 SET RENTED MACHINES = 4 FOR 8TH RUN MULTIPLE DEFINITION OF SYMBOL IN ABOVE CARD CLEAR CLEAR FOR 8TH RUN START 1 START THE 8TH RUN 1 CNTRL GENERATE ,,,55 SET RENTED MACHINES = 5 FOR 9TH RUN MULTIPLE DEFINITION OF SYMBOL IN ABOVE CARD CLEAR CLEAR FOR 9TH RUN START 1 START THE 9TH RUN END RETURN CONTROL TO OPERATING SYSTEM |
На основании результатов моделирования можно будет сказать, какие затраты несет производство при различных сочетаниях "нанимать/арендовать". Для фиксированного числа нанятых рабочих мастерской средние дневные расходы будут меняться в зависимости от числа арендуемых машин (рис. 2E.5). Рис.2Е.5 Зависимость дневных расходов от числа
арендуемых машин (число рабочих постоянно).
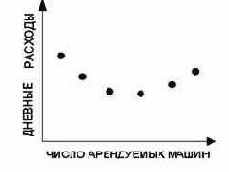
рабочих (число арендуемых машин постоянно)
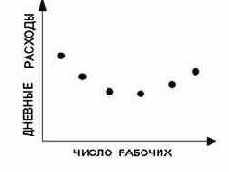
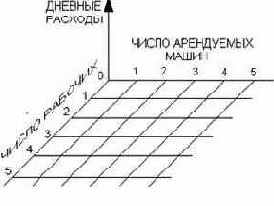
Поиск оптимального сочетания "число нанятых - число арендуемых" является, следовательно, поиском этой точки. Этот поиск можно осуществить различными методами. Рассмотрим два из них.
- Можно применить метод наискорейшего спуска. Этот метод заключается в выборе оптимального направления движения в области значений переменных по некоторому контуру до тех пор, пока не будут исчерпаны все возможные направления движения. Особенно удобно использовать этот метод либо при диалоговом режиме доступа к модели на ЭВМ через выносной пульт, либо если этот метод встроен в модель. В данной книге вторым методом мы пользоваться не будем.
- Модель может выполняться таким образом, что за каждый прогон определяется значение стоимости для одного соотношения значений "число нанятых - число арендуемых", и эти соотношения последовательно перебираются. Сначала можно исследовать довольно редкую решетку, так чтобы соотношения отстояли довольно далеко друг от друга. Рассмотрение результата обычно показывает, в какой области следует продолжать исследование. На следующем этапе моделирования исследуется ограниченная область с более близко расположенными значениями интересующего нас соотношения. Если необходимо, этот процесс можно продолжать, сужая область и делая решетку более частой. Так можно дойти до оптимального решения.
Кроме того, она сразу после ремонта возвращается в работу. Тогда каждая машина имеет средний цикл времени, равный 164 ч. Использование машины в такой идеальной системе равно примерно 95% [157/164 = 0,95]. Если в работе все время должно быть 50 машин (чтобы исключить потери из-за снижения объема производства), то общее число машин, циркулирующих в системе, должно быть равно 52,6 [52,6 Х 0,95 = 50 ]. При 50 работающих машинах 2,6 машины должны быть в резерве. Это, в свою очередь, означает, что следует нанять 2,6 рабочих. Приведенный расчет основан на некоторой идеализации системы. Конечно из-за наличия случайности в функционировании системы машины будут простаивать в двух местах, где ожидание потенциально возможно. Более того, арендовать 2,6 машины или нанять 2,6 рабочих невозможно. В результате приходим к выводу, что следует арендовать три, четыре или пять машин и взять на работу троих, четверых или пятерых рабочих. Это означает, что необходимо провести моделирование при девяти комбинациях, получающихся при переборе трех значений числа рабочих и трех значений числа машин. После того, как моделирование будет проведено, станет ясно, что наименьшую оценку стоимости дневных потерь дает соотношение "четверо рабочих - четыре резервные машины". Использование модели. Для моделирования использовали модель, представленную на рис. 2Е.2. Было осуществлено девять реконфигураций модели за один этап моделирования. Подготовленная колода карт для этого выглядела так, как показано на рис. 2Е.З. Обратите внимание на то, что карта 5 определяет емкость многоканальных устройств MEN и NOWON значениями 3 и 50 соответственно. Это соответствует трем нанятым рабочим и 50 одновременно работающим машинам. Карта 9 определяет блок GENERATE, через который в модель входят транзакты-машины. Операнд D равен 53, что соответствует наличию трех резервных арендуемых машин (операнд D равен сумме собственных и арендуемых машин). Блок GENERATE имеет символическое имя CNTRL (CoNTRoL, т.е. управление), поскольку этот блок должен переопределяться между картами START, когда необходимо отразить изменения в числе арендуемых машин.
После первой карты START карты 26, 27 и 28 соответственно изменяют модель (отражают реконфигурацию) и определяют четыре арендуемые машины, очищают модель от транзактов и сбрасывают статистику после первого прогона модели. Начинается моделирование при условиях "трое рабочих - четыре арендуемые машины". Карты 29, 30 и 31 повторяют эту процедуру и определяют соотношение "трое рабочих - пять арендуемых машин". Затем карта 32 переопределяет емкость многоканального устройства MEN на 4. Карта 33 модифицирует блок GENERATE с именем CNTRL, что снова определяет "три арендуемые машины". Далее модель очищается картой 34, а карта 35 начинает моделирование при соотношении "четверо рабочих - три арендуемые машины". Затем перебираются соотношения (4 - 4),(4 - 5),(5 - 3), (5 - 4), (5 - 5). Результаты моделирования. (Полное время моделирования на ЭВМ IBM 360/67 равнялось 68,2 с.) На рис.2Е.4 представлены выходные данные по многоканальным устройствам для первых трех изучаемых конфигураций системы. Для каждого многоканального устройства выдается семь различных типов информации. Рассмотрим их значения для многоканального устройства MEN (рис. 2Е.4, а).
- Моделировать три параллельно работающих прибора этого многоканального устройства, CAPACITY (ЕМКОСТЬ) =3.
- В среднем 2,185 из этих устройств были в состоянии занятости, AVERAGE CONTENTS (СРЕДНЕЕ СОДЕРЖИМОЕ) = 2,185.
- В среднем эти три прибора были загружены на 72,8%, AVERAGE UTILIZATION (СРЕДНЯЯ НАГРУЗКА) = 0,782.
- Общее число занятий приборов было 1924, ENTRIES (ВХОДОВ) = 1924.
- Среднее время на одно занятие было 7,087 единиц, AVERAGE TIME/TRAN (СРЕДHEE ВРЕМЯ/ТРАН) = 7,087.
- Ни один из приборов не находился в занятом состоянии в момент остановки моделирования, CURRENT CONTENTS (ТЕКУЩЕЕ СОДЕРЖИМОЕ) = .
- В процессе моделирования были моменты,когда все три прибора были в состоянии занятости одновременно, МАХIMUM CONTENTS (МАКСИМАЛЬНОЕ СОДЕРЖИМОЕ) = 3.
Отметим также, что в момент выдачи результатов (рис. 2Е.4,а) фабрика работала с полной нагрузкой, т.е. CURRЕNT CONTENTS (ТЕКУЩЕЕ СОДЕРЖИМОЕ) многоканального устройства NOWON было равно 50 Сопоставьте эти значения с аналогичными значениями на рис. 2Е.4, б и в. В табл.24.2(119) собраны величины нагрузки многоканального устройства NOWON как функции девяти различных значений соотношения "число рабочих - число арендуемых машин", определяемых моделью 2Е.3. Результаты соответствуют сделанным ранее предположениям. При заданном числе рабочих нагрузка растет при увеличении числа арендуемых машин. Аналогично этому при заданном числе арендуемых машин нагрузка растет при увеличении числа рабочих. Таблица 24.2. Нагрузка многоканального устройства как функция
различных соотношений "число рабочих - число машин".
| Число рабочих | Число арендуемых машин | ||
| 3 | 4 | 5 | |
| 3 | 0.983 | 0.989 | 0.992 |
| 4 | 0.989 | 0.993 | 0.997 |
| 5 | 0.991 | 0.993 | 0.997 |
различных соотношениях "число рабочих - число машин". а) Фиксированная плата
| Число рабочих | Число арендуемых машин | ||
| 3 | 4 | 5 | |
| 3 | 180 | 210 | 240 |
| 4 | 210 | 240 | 270 |
| 5 | 240 | 270 | 300 |
| Число рабочих | Число арендуемых машин | ||
| 3 | 4 | 5 | |
| 3 | 136 | 88 | 64 |
| 4 | 88 | 56 | 40 |
| 5 | 72 | 56 | 24 |
| Число рабочих | Число арендуемых машин | ||
| 3 | 4 | 5 | |
| 3 | 316 | 298 | 304 |
| 4 | 298 | 296 | 310 |
| 5 | 312 | 326 | 324 |

